Каталог статей
| Главная » Статьи » Сопромат |
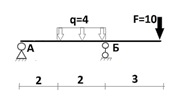
Теперь, когда мы разобрались, какие силы где возникают, можно перейти к их нахождению. Для примера возьмем обычную балку с минимумом сил, действующих на нее.
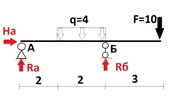
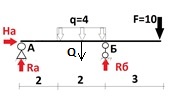
Что же действует на балку: cила F, которая равна 10 (не будем вдаваться в размерности, так как нам сейчас важно другое), распределенная нагрузка q, равная 4 и действующая на участке длиной 2, что видно на схеме. Балка стоит на двух шарнирах. В точке А неподвижный шарнир, в точке Б подвижный. Расставим силы, возникающие в шарнирах
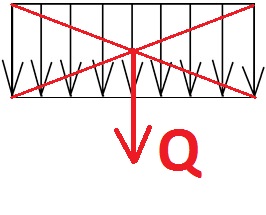
И так, в неподвижном возникает две силы На и Ra, в подвижном только одна – Rб. Для их нахождения разберемся с распределенной нагрузкой, что это такое и как оно вообще действует. Изображается она по-разному
Но чаще всего вот так
Если сказать простыми словами – это множество сил, натыканных на каком-то определенном участке. Нам нужна длина этого участка и интенсивность нагрузки. В нашем случае длина участка с распределенной нагрузкой равна 2 , а интенсивность это q , и она равна 4. Наша распределенная нагрузка представляет собой прямоугольник. Для нахождения опорных реакций в шарнирах, мы можем заменить распределенную нагрузку на обычную силу. Мы знаем как найти центр тяжести прямоугольника – это пересечение двух диагоналей, именно из центра будет идти наша сила
Назовем ее Q большое, т.к. распределенная нагрузка q маленькое. Чему же равно Q большое? Все очень просто: это произведении длины участка на интенсивность Q=q*L. В нашем случае Q будет равно 4*2=8 (интенсивность q=4, длина участка, на который действует нагрузка равен L=2, отсюда Q=8) Стоит учитывать, что нагрузка может быть не в виде прямоугольника, так же встречаются распределенные нагрузки в виде треугольника, трапеции, где центр тяжести находится по другим формулам. Вернемся к нашей балке.
Мы указали найденную Q (это делать не обязательно) и теперь можем приступить к нахождению неизвестных реакций. Начнем с На. Дело в том, что нахождение реакций сводится к нахождению суммы проекций сил на оси Х и Y. И в данном случае на ось Х действует только одна сила – На, следовательно она равна 0. Распишем подробнее. ∑Fx=0 Сумма всех сил на ось Х равна 0. Теперь распишем все силы, действующие на эту ось. Стоит учесть, что силы действующие вправо по оси Х – положительные, а влево – отрицательные, а по оси Y – вверх положительные, вниз отрицательные. Можно задать и по другому, но во всех учебниках идет именно такое обозначение. На=0 это мы расписали все силы, действующие на ось Х, в нашей схеме она только одна – На. Теперь, если мы распишем сумму всех сил на ось Y, то у нас получится два неизвестных, и это нужные нам Ra и Rб. В этом случае нам следует расписать не сумму сил, а сумму моментов относительно какой-либо точки. Возьмем сумму моментов относительно точки А. ∑МА=0 Теперь нам нужно расписать все моменты, действующие относительно этой точки. Моментом является сила, умноженная на плечо. Плечом будет расстояние от линии действия силы, до точки, относительно которой мы рассматриваем сумму моментов. Мы выбрали точку А.
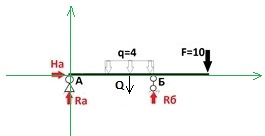
Эти линии – линии действия сил. Синяя линия действия силы Ra, голубая – Q, зеленая Rб, желтая – F и красная – Ha. Момент, как мы уже сказали, это произведение силы на плечо, смотрим на плечи. У сил Ra и Hб плечи равны 0, т.к. эти силы действуют в самой точке А. Смотрим на плечо Q, оно равно 3, т.к. от точки А до начала действия распределенной нагрузки расстояние 2, распределенная нагрузка длиною тоже 2, но равнодействующая Q находится по середине распределенной нагрузки, значит 2/2=1 и в итоге 2+1=3 наше плечо С плечом у Rb все понятно, оно равно 4, с плечом F все то же просто – оно равно 7. Если бы в балке присутствовал отдельный изгибающий момент, то мы бы вносили его в сумму моментов без плеча, не зависимо от того, на каком расстоянии от точки он приложен. В термехе есть такое правило знаков: Момент, вращающийся по часовой стрелке – отрицательный, против часовой стрелки – положительный. Этим правилом мы и будем пользоваться в решении. Чтобы понять, в какую сторону та или иная сила вращает нашу нагрузку, мысленно проведем оси, с началом координат в точке А.
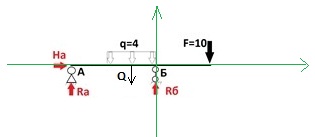
И теперь гораздо проще понять в какую сторону силы вращают конструкцию. То есть мы как будто забили в начало координат гвоздь и смотрим, кто куда будет вращать нашу конструкцию относительно забитого гвоздя. Q вращает по часовой, Rб против часовой и F по часовой стрелке. Следуя этому мы расставляем знаки ∑МА=0 -Q*3+Rб*4-F*7=0 Подставляем цифры вместо букв. -8*3+Rб*4-10*7=0 Rб*4=24+70 Rб*4=94 Rб=94/4 Rб=23.5 Таким образом мы нашли Rб. Теперь нам нужно найти Ra, и мы распишем сумму моментов относительно точки Б.
∑МБ=0 Смотрим плечи и направления вращения. На не действует, т.к. нет плеча, линия действия силы совпадает с нашей точкой. Ra действует по часовой стрелке с плечом 4. Q против часовой стрелки с плечом 1. F по часовой стрелке с плечом 3. Расписываем: -Ra*4+Q*1-F*3=0 Подставим цифры вместо букв: -Ra*4+8*1-10*3=0 8-30=Ra*4 -22=Ra*4 Ra=-22/4 Ra=-5.5 Нашли Ra. Сила получилась отрицательной. Сила может быть отрицательной, это значит, что мы на чертеже указали ее не в том направлении, то есть она должна идти не вверх, а вниз, и тогда она будет положительной. В нашем решении мы оставим все так, и в дальнейшем исправлять ничего не нужно, так как мы рассматриваем один знак и одно направление. Мы нашли все неизвестные нам силы. Теперь стоит проверить, правильно ли мы их нашли. Выполним простую проверку, распишем сумму сил на ось Y. ∑FY=0 Ra+Rб-Q-F=0 Подставим значения -5,5+23,5-8-10=0 0=0 Проверка выполнена, значит реакции мы нашли правильно. | |
| Просмотров: 5097 | |
| Всего комментариев: 0 | |