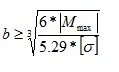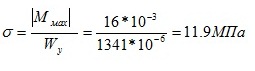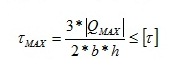Каталог статей
| Главная » Статьи » Сопромат |
В расчетно-графической работе необходимо подобрать сечение прямоугольной формы. В условии нам дано отношение сторон прямоугольника β=h/b , допустимое нормальное напряжение [σ] и допустимое касательное напряжение [τ]. Не будем вдаваться в теорию, для решения в ней нет большой необходимости, все решается элементарно по формулам. Во всех вариантах у нас дано: [σ]=12 Мпа [τ]=2 Мпа А вот β во всех вариантах разная, мы возьмем β=2,3 Задача состоит в том, чтобы найти стороны прямоугольника, вычислить максимальные напряжения и сравнить их с допустимыми. Приступим. Существует формула требуемого момента сопротивления:
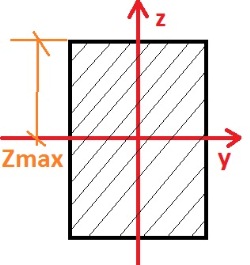
Для прямоугольника момент инерции находится по формуле:
А Zmax ни что иное, как половина длины h
Из этого формула получает вид: Из соотношения сторон можно выразить одну сторону, через другую, к примеру выразим h h=b*2.3 Теперь подставим это h в полученную выше формулу момента сопротивления Wy
Так как
Ммах мы смотрим по нашим эпюрам, какое будет максимальное значение моментов. Отсюда выражаем b
Подставляем значение М. В прошлых уроках, где мы решали балку и строили эпюры Ммах=16 кН*м Но нам нужно соблюдать размерность, т.к. [σ] в Мпа. 16 кН*м = 16*10-3 Мпа*м2 Подставляем значение в формулу и получаем ответ: b=0.1147 м=11,5 см Находим h из соотношения сторон h=11,5*2.3=26,45 см Теперь , когда мы нашли обе стороны прямоугольника, нам нужно рассчитать момент сопротивления Wy
Теперь мы можем определить фактическое значение нормального напряжения:
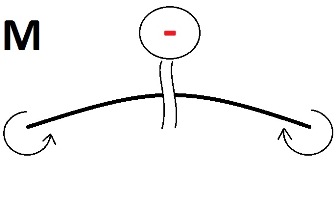
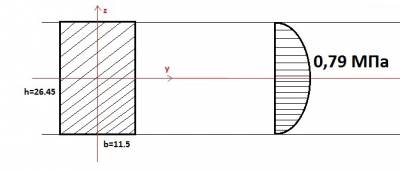
Мы вычислили напряжения. Теперь нам нужно построить их эпюру Вот таким образом выглядит эпюра. Что стоит учесть: по середине напряжения равны 0, на обоих краях они максимальные и равны 11,9 – т.е. найденному нами значению. Что означают знаки + и – в наших эпюрах? При расчетах мы использовали максимальный момент, и стоит посмотреть, с каким он был знаком. Если знак положительный – это значит, что балка в данном сечении изгибается в таком виде А если отрицательный, то в таком У нас был момент равен -16, и балка в этом сечении принимает вид, как на втором рисунке. Это значит, что верхние волокна растянуты, а нижние сжаты (это видно на рисунке). При растяжении длина волокон увеличивается, при сжатии – уменьшается. Собственно на эпюре мы и указываем в каком месте у нас волокна растянуты – знак плюс, а в каком сжаты – знак минус. Далее нам нужно проверить прочность балки по касательным напряжениям. Для этого с нашей балки из прошлого урока нужно узнать максимальную поперечную силу QMAX . Ее мы можем посмотреть на эпюре, которую мы строили в том уроке. Как ни странно, но максимальная поперечная сила, так же как и момент, равна 16кН. Для расчета существует специальная формула:
То есть, максимальное касательное напряжение должно быть меньше, чем допустимое. Подставляем наши значения, учитывая размерности
0,79 МПа меньше, чем допустимое 2МПа. И вот теперь нам осталось построить эпюру касательных напряжений. Она легче, чем эпюра нормальных напряжений, так как не надо учитывать растягивается балка или сжимается, а значит нет мороки со знаками. Эпюра представляет собой что-то вроде дуги. На концах касательное напряжение равно 0, а в середине оно максимальное и равное найденному нами значению. Таким образом мы подобрали прямоугольное сечение для нашей балки, нашли касательное и нормальное напряжение в сечении и построили их эпюры.
| |
| Просмотров: 7569 | |
| Всего комментариев: 0 | |
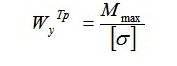
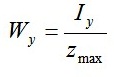 общая формула для момента сопротивления
общая формула для момента сопротивления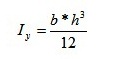
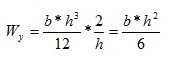
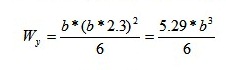
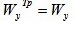 мы записываем
мы записываем