Каталог статей
| Главная » Статьи » Сопромат |
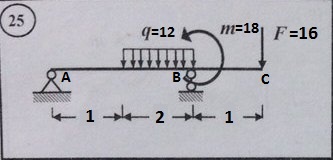
Расчет балки на прочность и построение эпюр – это вторая расчетно-графическая работа по сопротивлению материалов (РГСУ). Сейчас мы рассмотрим часть этой расчетно-графической работы, а именно построим эпюры изгибающих моментов и поперечных сил. Примером будет балка, взятая из условий расчетно-графических работ
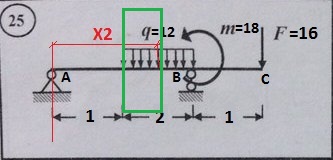
Для начала нужно найти опорные реакции, это мы уже делали в прошлых уроках, так что без объяснений, только решение: ∑МА=0 -q*2*2+Rb*3+m-F*4=0 -12*2*2+3*Rb+18-16*4=0 -48+18-64+3*Rb=0 3*Rb=94 Rb=94/3 Делить не будем, т.к. конечного числа не получается. ∑МВ=0 -Ra*3+q*2*1+m-F*1=0 -3*Ra+12*2*1+18-16*1=0 26=3*Ra Ra=26/3 Проверка ∑FY=0 Ra+Rb-q*2-F=0 26/3+94/3-12*2-16=0 120/3-24-16=0 40-40=0 0=0 Проверка выполнена, опорные реакции найдены правильно. Что делать дальше? А дальше мы смотрим, на сколько участков разбита наша балка. По идее участок заканчивается где начинает действовать другая сила, но гораздо проще смотреть количество участков по данным нам длинам. Нам дано 3 длины, значит участка тоже будет три. Приступаем. Первый участок можно брать хоть слева, хоть справа. Мы пойдем слева направо. Собственно вот наши участки:
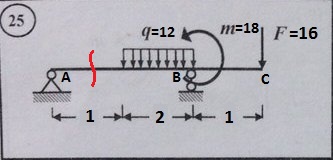
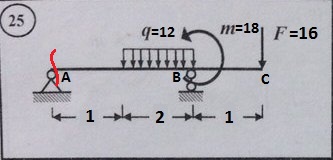
В красном прямоугольнике первый участок, в зеленом – второй, в синем – третий. И так, первый участок. Мысленно проводим сечение
На чертеже оно, можно сказать, по середине участка, но не стоит забывать, что сечение изменяется от начала участка
До конца
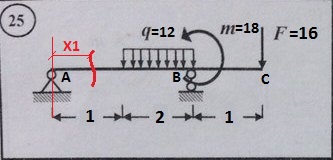
И оно может находится в любом месте, в пределах первого участка. От начала участка, до сечения расстояние Х1
Если мы сказали, что сечение может быть в любой точке первого участка, то и Х может принимать разные значения, именно поэтому мы задаем для него границы: 0≤Х≤1 Х может принимать значения от 0 до 1 т.к. весь участок длиной 1. Теперь мы смотрим, какие же силы действуют на нашем участке. Кроме реакции опоры Ra ничего не действует (q не попадает в наш участок).
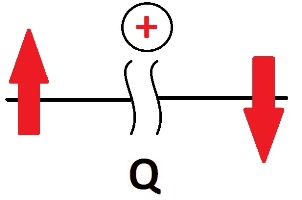
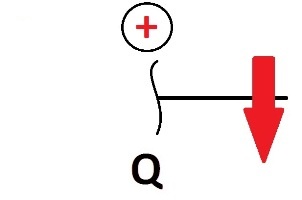
Для поперечных сил существует правило знаков:
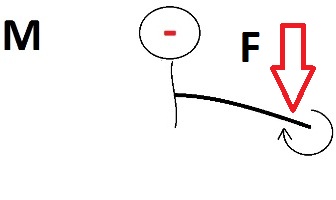
По середине идет сечение. Смотрим на наше сечение. Все, что левее сечения мы отбрасываем, его как бы нету. На первом участке нас интересует лишь то, что входит в этот участок. У нас есть Rа, оно направлено вверх (Реакция опоры), прямо как на первом рисунке правил знаков, следовательно знак будет + QХ1=Ra=26/3=8,7 кН (теперь лучше поделить) пишем так же размерность, для Q это килоньютоны. Далее нам надо найти М на первом участке. Для М есть свое правило знаков:
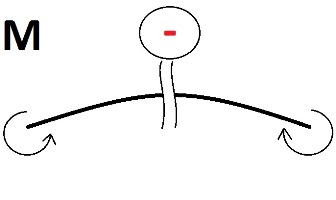
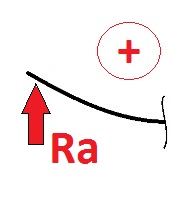
Это правило называют правилом «дождя», если сверху «вылить воду», то на первом рисунке вода останется налита, как в тарелку, а на втором рисунке она просто стечет. Вода осталась, значит у нас есть что попить, а это явный плюс для нас :) . На рисунке два мы остались без воды, а это уж точно не плюс, а скорее минус. Чистых моментов на первом участке нету. Момент будет давать лишь опорная реакция Ra. Как помним, момент это сила умноженная на плечо. Плечом у нас будет расстояние X1. Записываем Мx1=Ra*X1 Почему знак + ? Теперь мы смотрим в какую сторону гнет нашу балку эта сила, если она направленна вверх, то по логике она изгибает балку прямо как на первом рисунке правил знаков для моментов, а именно
Теперь вместо X1 мы подставляем пределы нашего участка (0≤Х≤1) которые мы записывали вначале МХ1=0=8,7*0=0 МХ1=1=8,7*1=8,7 кН*м Первый участок сделан, переходим к участку номер два. Как и в первом участке пишем пределы 1≤Х2≤3 Почему от 1 до 3 , а не от 0 до 2 ?
Да потому, что мы не можем брать от 0 до 1, т.к. это границы первого участка, а второй участок начинается с 1 и идет до 3. QX2=Ra-q*(X2-1) Теперь сложный момент с распределенной нагрузкой. В наше сечение попадает лишь его часть:
Если подумать, то она равняется Х2-1 вот тот участок, где действует нагрузка Q. Почему она с минусом: ну во-первых она гнет балку вниз, а во-вторых она противоположна по направлению положительной Ra, следовательно она будет с другим знаком. Теперь мы подставляем наши границы в получившееся уравнение: QX2=1=8,7-12*(1-1)=8,7 кН QХ2=3=8.7-12(3-1)=-15.3 кН А вот здесь есть не большой, но важный момент: у нас Q поменял знак на участке с плюса на минус (может менять наоборот), а это значит, что на этом участке момент будет приобретать экстремальное значение и его нам придется найти. МХ2=Ra*X2-q*(X2-1)2/2 Почему для моментов такое странное уравнение? Все очень просто: q действует на участке равном (Х2-1) , плечом этой силы будет (Х2-1)/2 и это все нужно перемножить q*(X2-1)*(X2-1)/2 Подставляем значения Х2 МХ2=1=8,7*1-12*(1-1)2/2=8,7 кН*м МХ2=3=8,7*3-12*(3-1)2/2=26,1-24=2,1 кН*м Теперь нам нужно найти тот самый экстремум, про который говорилось ранее. Для этого нам нужно приравнять 0 уравнение поперечных сил Q для этого участка и найти значение X2: Q=Ra-q*(X2-1)=0 8,7-12*X2+12=0 20.7=12*X2 X2=1.725 Теперь найденное значение Х2 мы подставляем в уравнение моментов М и находим нужный нам экстремеум. Всю эту процедуру важно запомнить! МХ2=1.725=8,7*1,725-12*(1,725-1)2/2=15-3,2=11,8 кН*м (это мы потом укажем на эпюре)
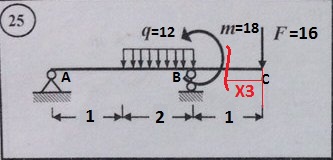
Со вторым участком покончено. Остался один. Его можно рассмотреть так же – слева направо, но придется учитывать все опорные реакции, нагрузку и момент, а можно рассмотреть его справа и нам нужно будет учесть только силу F. Так мы и поступим:
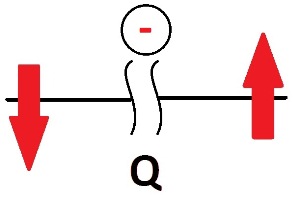
Вот он, наш третий участок. Указываем границы: 0≤Х3≤1 (мы рассматриваем участок справа, а он начинается от 0 и заканчивается 1) Запишем уравнение поперечных сил: QX3=F=16 кН почему плюс? Смотрим правило знаков:
Смотрим относительно сечения по правилу знаков. Теперь уравнение моментов: МХ3=-F*X3 Знак не такой как в уравнении Q, а кто сказал, что они должны быть всегда одинаковыми? Мы пользуемся правилами знаков для моментов М:
Наша сила F гнет балку вниз, а значит знак минус. Подставляем границы: МХ3=0=0 МХ3=1=-16 кН*м
Вот мы рассчитали все участки, дальше построение эпюр.
| |
| Просмотров: 2947 | |
| Всего комментариев: 0 | |